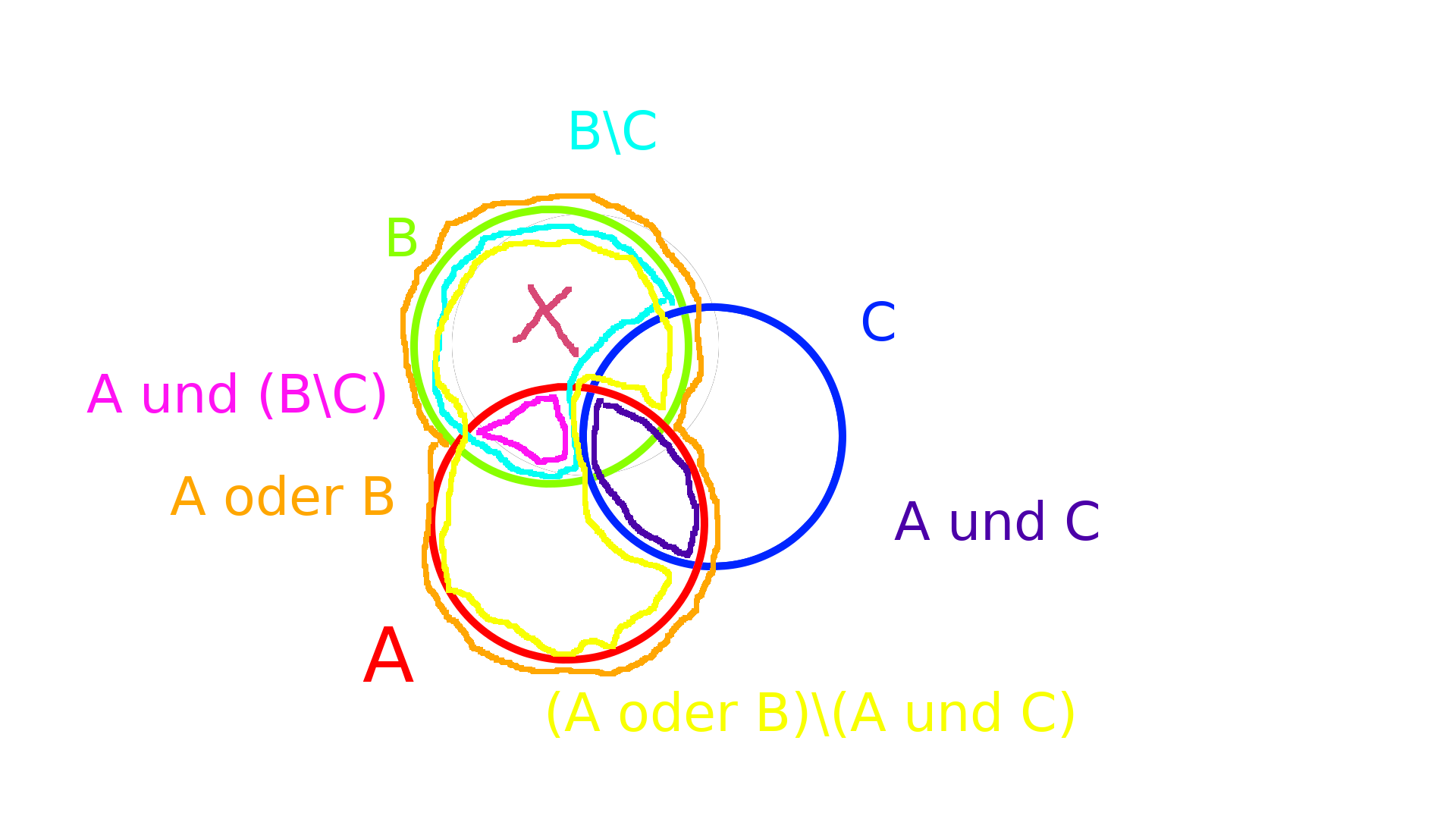
 Das pinke Kreuz ist in \((A\cup B)\backslash(A\cap C)\), aber nicht in \(A \cap(B\backslash C)\)
Das pinke Kreuz ist in \((A\cup B)\backslash(A\cap C)\), aber nicht in \(A \cap(B\backslash C)\)| Gruppennumer | Übungsleiterin | Übungsnummer | Name |
|---|---|---|---|
| 10 | Eya Chemangui | 01 | Roman Gräf |
Bitte H1.1 und H1.2 bewerten.
\(\exists x \in \mathbb{Z} | \forall y \in \mathbb{Z} | y \leq x\)
Negation: Die Menge der ganzen Zahlen besitzt kein größtes Element \(\neg (x \in \mathbb{Z} | \forall y \in \mathbb{Z} | y \leq x) \iff \forall x \in \mathbb{Z} | \exists y \in \mathbb{Z} | x \leq y\)
\(\forall x \in \mathbb{N} | [(x = 0) \lor(\exists n \in \mathbb{N}|x = n + 1)]\)
Die Relation \(R\) genau dann eine Totalordnung auf einer Menge \(X\) ist, wenn sie für jede zwei Elemente von \(X\) mindestens einen Eintrag (x,y) oder (y,x) enthält. Da \(R\) der Durchschnitt von \(R_1\) und \(R_2\) ist, müssen sowohl \(R_1\) als auch \(R_2\) alle für jedes \(x\in X,y\in X\) genau entweder \((x,y)\) oder \((y,x)\) enthalten.
\(\neg(A\land B)\iff (\neg A) \lor (\neg B)\)
| \(A\) | \(B\) | \(\neg(A\land B)\) | \((\neg A) \lor (\neg B)\) |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
Wahrheitstabellen stimmen überein.
\(\neg(A\lor B)\iff (\neg A) \land (\neg B)\)
| \(A\) | \(B\) | \(\neg(A\lor B)\) | \((\neg A) \land (\neg B)\) |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
Wahrheitstabellen stimmen überein.
\([A\implies B]\iff [(\neg B)\implies(\neg A)]\)
| \(A\) | \(B\) | \(A \implies B\) | \((\neg B)\implies(\neg A)\) |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Wahrheitstabellen stimmen überein.
| \(A\) | \(B\) | \(A \implies B\) | \(B\implies A\) |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Wahrheitstabellen stimmen nicht überein.
Alle Wände die ein Fenster haben.
Negiert: \(\exists x \in W | \neg F(x)\)
Es gibt eine Wand die kein Fenster hat.
Alle Wände die Türen haben, haben keine Fenster.
Negiert: \(\exists x \in W | (T(X)\land F(X))\) Es gibt eine Wand die sowohl Tür als auch Fenster hat.
 Das pinke Kreuz ist in \((A\cup B)\backslash(A\cap C)\), aber nicht in \(A \cap(B\backslash C)\)
Das pinke Kreuz ist in \((A\cup B)\backslash(A\cap C)\), aber nicht in \(A \cap(B\backslash C)\)
\[M = \mathbb{N} \\ R = \lbrace(n,m) \in M \times M | n = m\rbrace\]
\[M = \lbrace0,1\rbrace \\ R = \lbrace(0,1)\rbrace\]
\[M = \lbrace0,1\rbrace \\ R = \lbrace(0,1),(1,0)\rbrace\]