Übungsblatt 01

Aufgabe H1.1

a)

b)

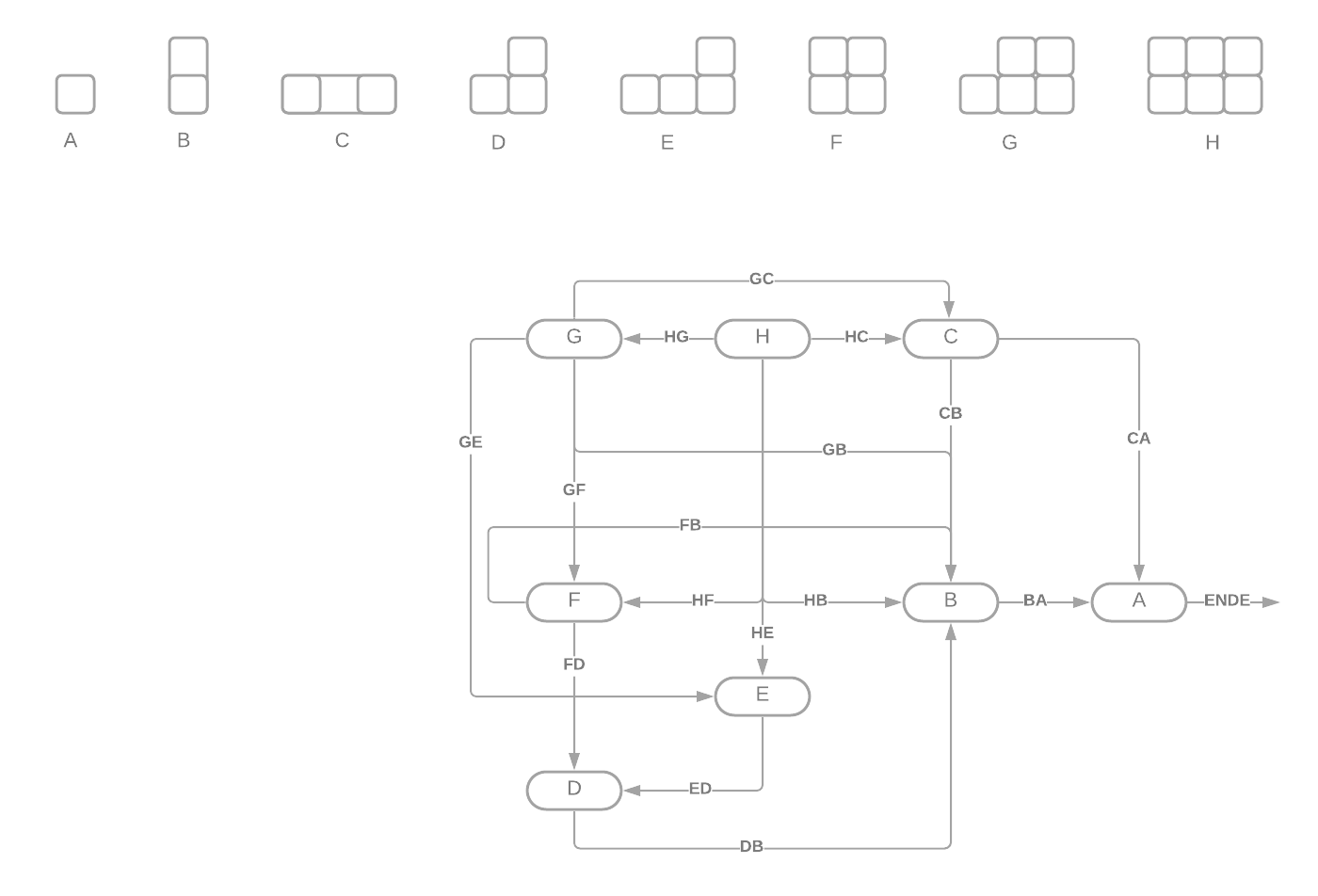
Die Position A ist eine Verlier-Position. Durch das Essen des letzten Stückes verliert man und es führt kein Weg daran vorbei. Eine Gewinnposition wäre eine, die den Gegner in Position A bringen kann, z.B B oder C. Dadurch ist auch D eine Verlier-Position da es in der Position keinen anderen Optionen gibt als den Gegner in eine Gewinnposition zu bringen. Durch E und F kann man den Gegner in Position D zwingen. Somit sind diese Gewinnpositionen. Position G erlaubt es lediglich den Gegner in Gewinnpositionen bringen zu können, daher ist G eine Verlier- Position.

c)

Derjenige der anfängt kann immer gewinnen indem er/sie zu Beginn (H) das Stück oben links isst und den Gegner damit in die Verlier-Position G bringt. Der Gegner muss wählen zwischen B,C,E oder F; Er befindet sich stets in einer Verlier-Position, während der/die beginnende Spieler/in sich immer in einer Gewinnposition befindet.

Aufgabe H1.2

Aufgabe a)

• 1. Die Relation \(R_1\) ist nicht reflexiv. Beispiel: \(\lbrace a\rbrace\)
• 2. Die Relation \(R_2\) ist reflexiv, symmetrisch und transitiv \(\implies\) eine Äquivalenzrelation.
• 3. Die Relation \(R_3\) ist reflexiv, symmetrisch und transitiv \(\implies\) eine Äquivalenzrelation.

Aufgabe b)

• 2. Die Relation \(R_2\) ist verträglich mit der Konkatenationsoperation.
• 3. Die Relation \(R_3\) ist nicht verträglich mit der Konkatenationsoperation.

Gegenbeispiel:

\(u_1 = ababa\) \(v_1 = babab\) \(u_2 = abba\) \(v_2 = abba\)

\[(u_1,v_1)\in R_3\text{ und }(u_2,v_2) \in R_3\text{ aber }(u_1u_2, v_1v_2) \notin R_3\]

Aufgabe H1.3

\[T(n)=\frac{n\cdot(n+1)}{2}\] \[f(x,y)=T(x+y)+x=T(m)+x\]

Für ein gegebenes \(n\in\mathbb{N}\) wähle man das größtmöglichste \(m\in\mathbb{N}\) so, dass \(T(m)\le n\) gilt, sowie \(x=n-T(m)\). Da \(T(m)\le n<T(m+1)\): \(x=n-T(m)<T(m+1)-T(y)=m+1\), d.h. das \(y=m-x>0\). Dementsprechend existiert für jedes \(n\) mindestens ein Paar \((x,y)\) für das \(f(x,y)=n\) gilt.

Angenommen es existeren \((x,y),(i,j)\in\mathbb{N}\times\mathbb{N}\), so dass \(T(x)+y=T(i)+j\), mit \(x\le y\land i\le j\) und \(x\le i\). \(T(n)\) kann als \(\sum_{m=1}^{n}m\) neuschreiben (siehe Gaussche Summenformel). \[y+\sum_{n=1}^{x}n=\sum_{n=1}^{i}n+j\] \[y-j=\sum_{n=x+1}^{i}n\]

Falls \(x<i\), dann muss \(y-j=0\) sein \(\implies y=j\implies T(x) = T(i)\implies i=x\). Ansonsten \(x=i\implies y=j\).

Dementsprechend ist es eindeutig.

Da sowohl injektivität als auch surjektivität bewiesen sind, ist die bijektivität bewiesen.

Funktion g

Die Funktion \(f\) erhält ein 2-Tupel natürlicher Zahlen \(x\) und \(y\) und bringt sie zu einem Wert \(w\in\mathbb{N}\).
Für die Eingabe \(f(w,z)\) mit \(z\in \mathbb{N}\) erhalten wir also ebenfalls ein singuläres Ergebnis. Bringen wir nun \(w\) in seine Ursprungsform \(f(x,y)\) so erhalten wir \(f(f(x,y),z)\), welches auch bijektiv ist. Damit verknüpft es 3 Elemente aus \(\mathbb{N}\), man könnte es also auch schreiben als Funktion \(g(x,y,z)\), welche eine Bijektion von \(\mathbb{N}\times\mathbb{N}\times\mathbb{N} \longmapsto \mathbb{N}\) darstellt.
\(g(x,y,z)=\frac{(f(x,y)+z)\cdot(f(x,y)+z+1)}{2}+f(x,y)\)